I want to know how to model that every individual must get at least one night shift break, and must not work two consecutive shifts. Finally, we want to ensure as close to equal numbers of night shifts and total shifts for each individual as possible.

Problem descriptions

    1. 8 Individuals
    2. 3 Shifts per day (morning, afternoon, night)
    3. 18 Days

Specifications

    1. There must be 3 people on each shift
    2. Every individual must work 1 shift per day
    3. Every individual must not work more than 2 shifts per day
    4. Every individual must get at least one night shift break, preferably two. This means that individual A can work night shift 1, but then cannot work night shift 2 (and preferably not 3), returning to night shift 4. I.e. each individual must do a maximum of 1 night shift in every 2 nights, preferably 1 night shift in every 3 night shifts.
    5. We should distribute these shifts as evenly as possible, especially night shifts but also the total number of shifts.
    6. Each individual must not work consecutive shifts (e.g. the night shift on Day 1 and the morning shift on Day 2)

Day Definition

For example, we defined “ThisMonth” for 18 days from Jun.1.2022 to Jun.18.2022.



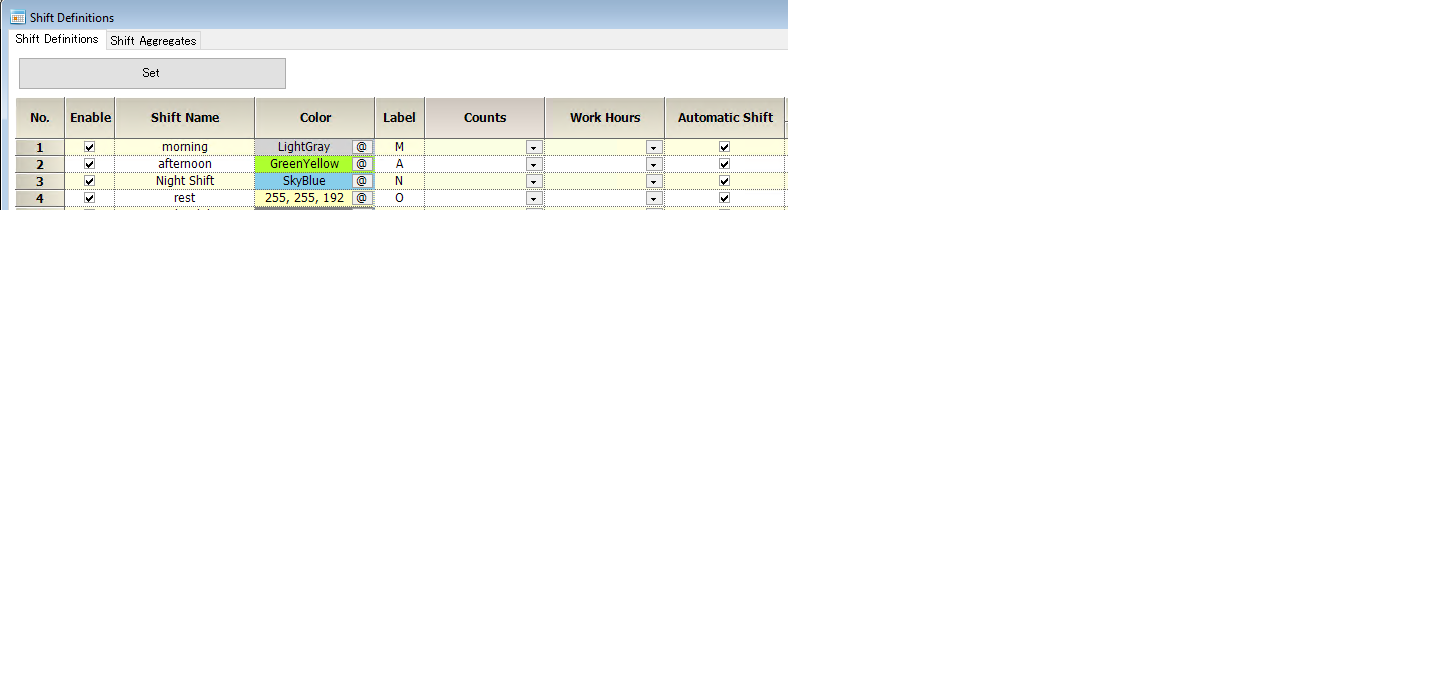
Shift Definitions

The first is to define shifts, morning, afternoon, and night. In addition to explicit works, we should define the rest as a shift.



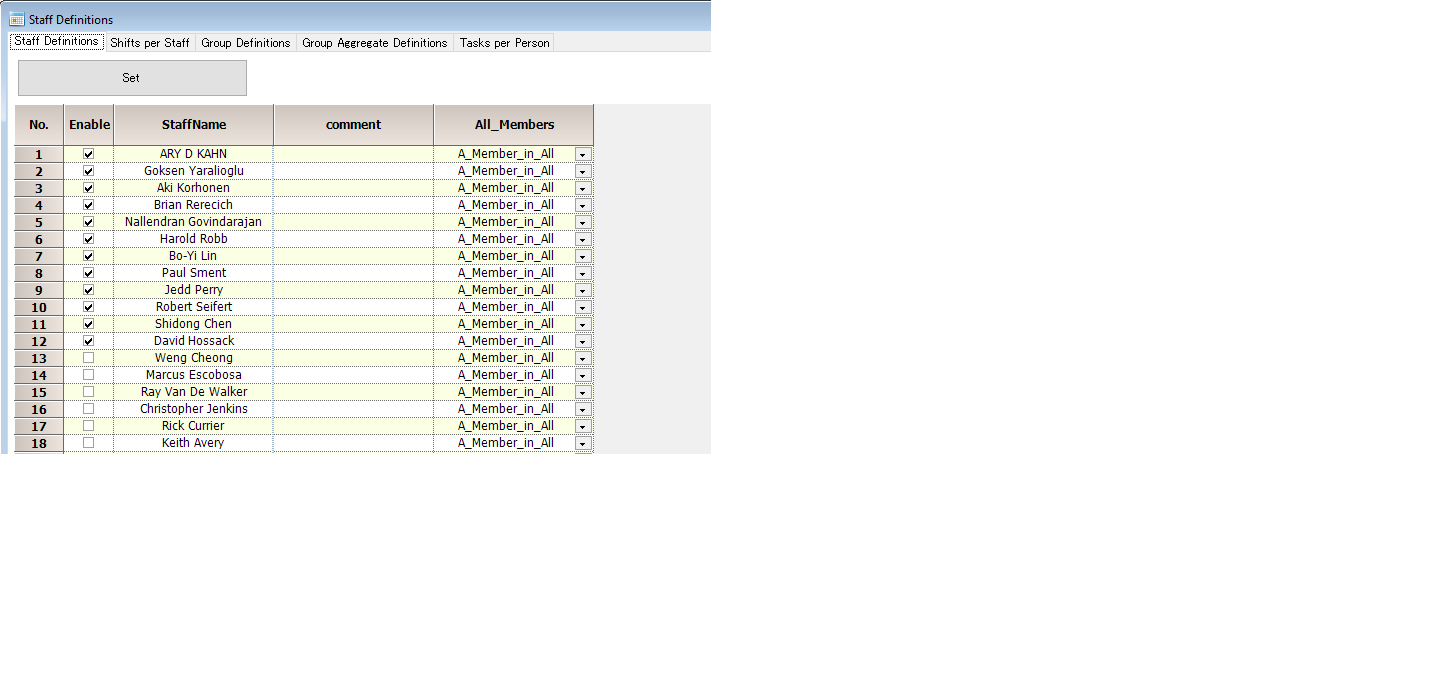
Staff definitions

The next is to define eight people from the specification.



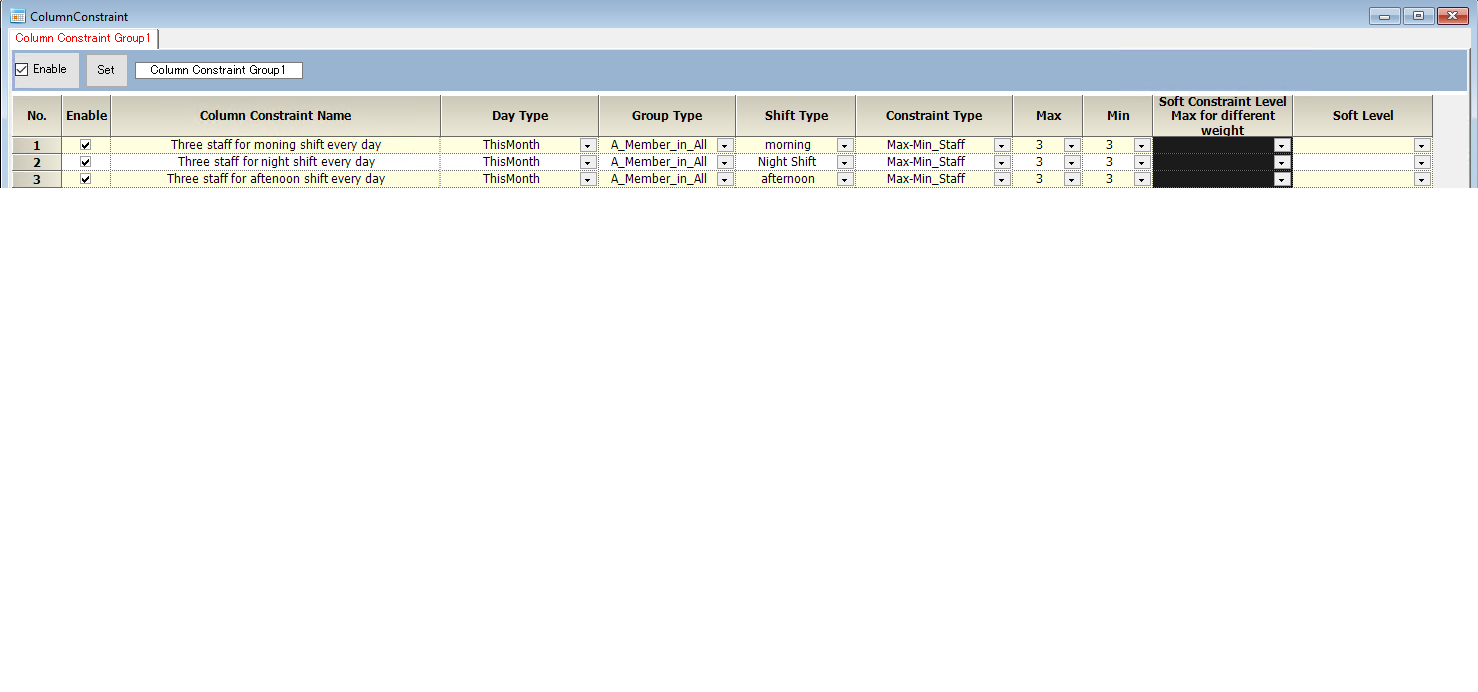
Cover constraints

The specification requires three staff for each shift.



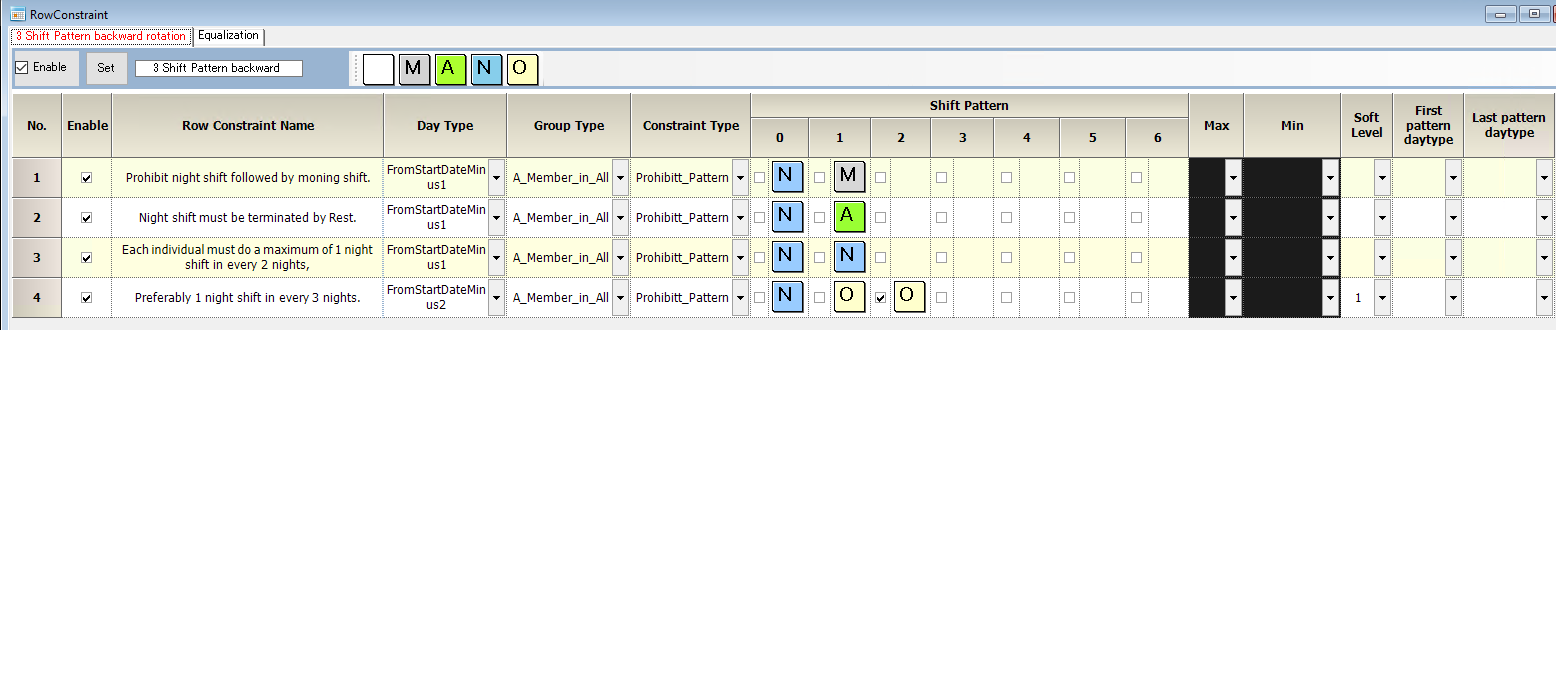
Row constraints

Pattern Constraints

Each individual must do a maximum of 1 night shift in every 2 nights.
Every individual must get at least one night shift break, preferably two.
These two constraints are hard.

Preferably 1 night shift in every 3 night shifts
“Preferably” usually means using a soft constraint.



Number of shifts

These constraints depend on the number of staff. Therefore, after determining the number of staff, we define these numbers.

Consideration for cover requirements.

Each shift requires three staff per day, so
9 staff * 18 days=162 shifts will be the total shift amount.
On the other hand, total shifts available from staff resource is 1 * 18 days*8 staff=144 shifts.

Note 144 < 162 inevitably results in no solution.

We need more staff than eight staff.

9 staff is enough for a solution?

If we have nine teams, then 9*18 days=162 shifts, equal to minimum cover requirements. However, we have hard row constraints, such as ;

    1. Every individual must get at least one-night shift break.
    2. Each individual must do a maximum of 1-night shift in every 2 nights.
These constraints should increase required staff resources. The problem is we are not sure how much we need more staff.

Feasible solution

We need a feasible solution before we optimize.
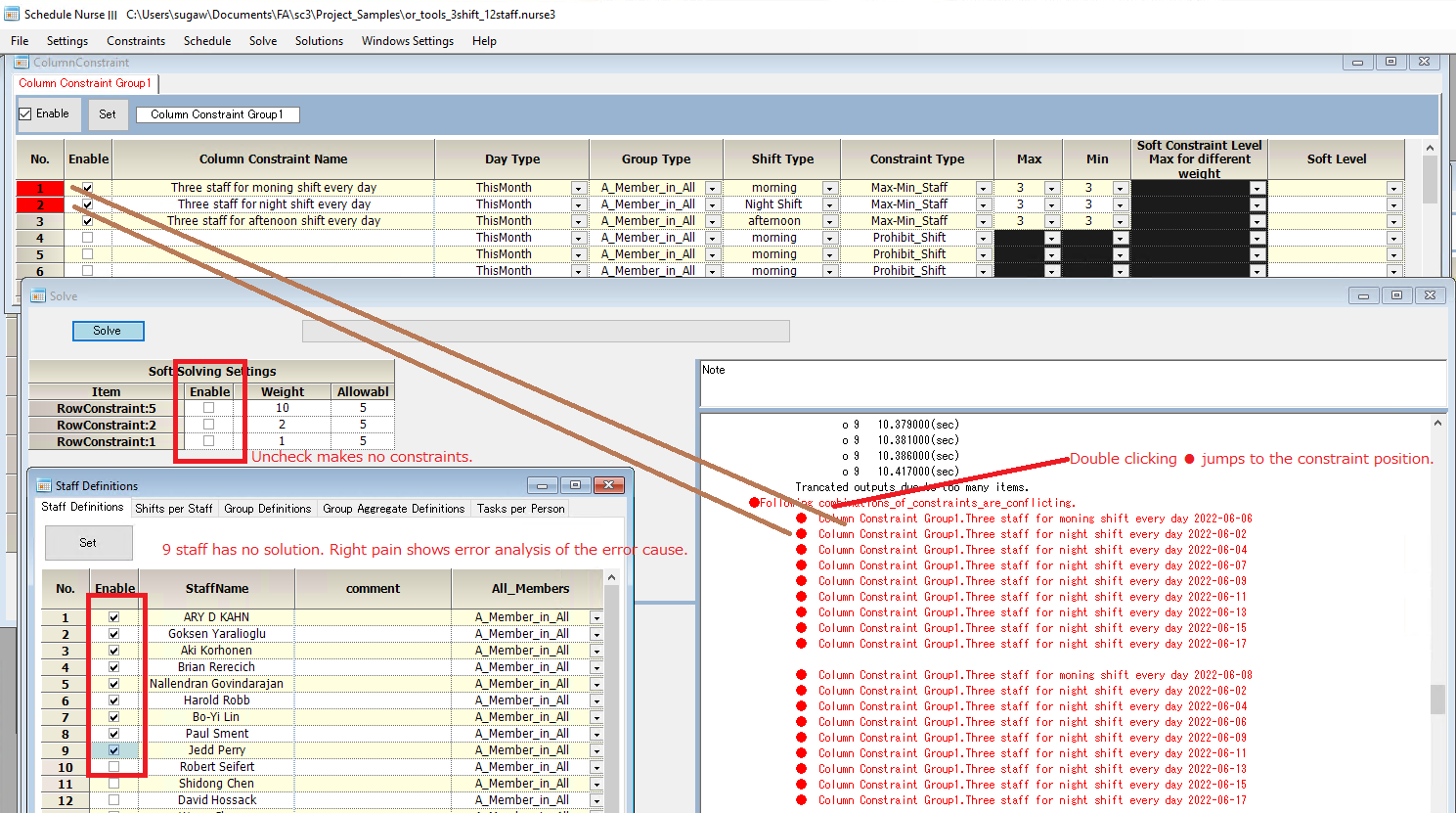
We tried to solve by 9,10, and 11 staff but could not find any solution.

Fig. below shows the cause of the no solution analysis.
This routine automatically invokes if Schedule Nurse 3 found there is no solution or could not find an answer in the specified timeout.

Clicking the Red mark ● jumps the position of cause to the constraint. We did the operation with empty soft row constraints. (Unchecked mark means no rules applied for the item.)



Row constraints optimization

Finally, 12 staff got a solution.

Since required shifts are 3*18=54shifts, 54 shifts/ 12staff =4.5(avg.), we constraint 4<=x<=5 for each shift per staff.
The spec. says;
5. We should distribute these shifts as evenly as possible, especially night shifts but also the total number of shifts.



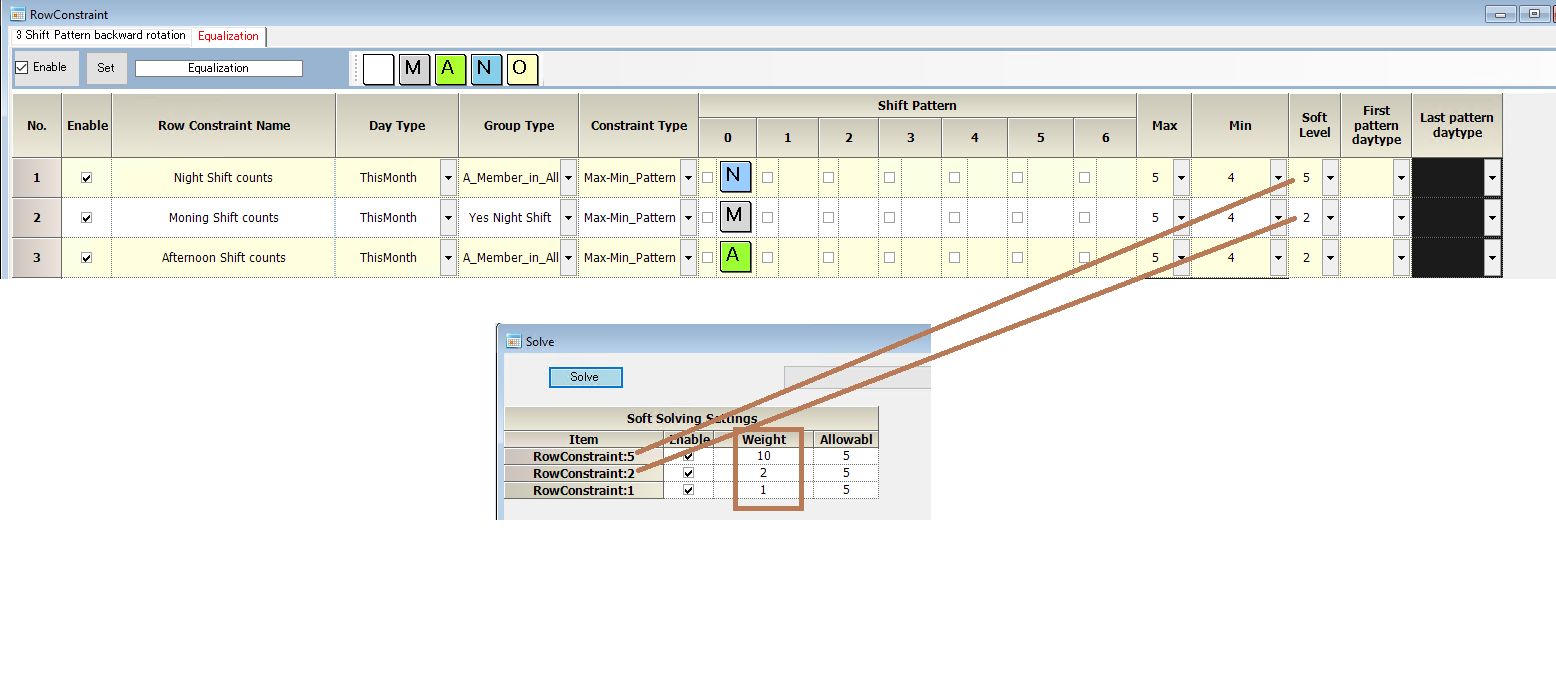
So, we have a higher penalty(weight 10) for the night shift.

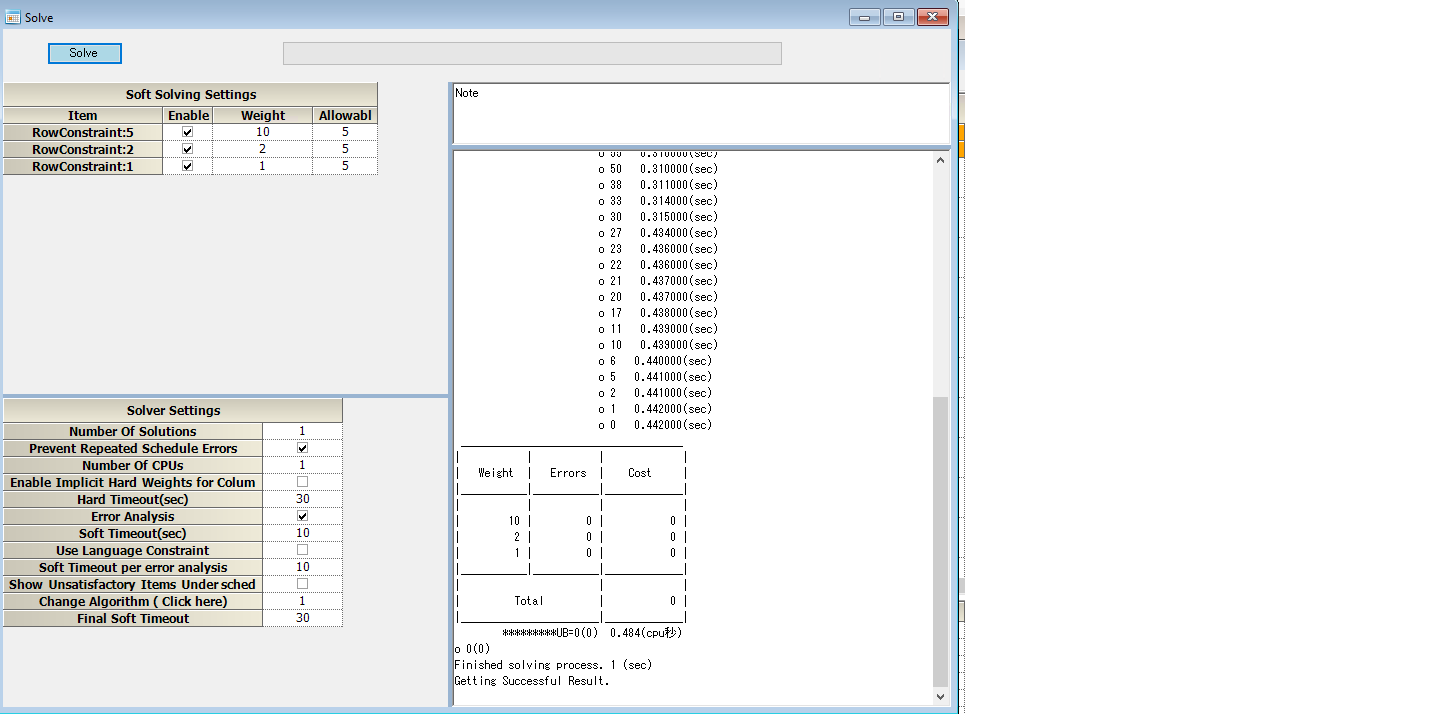
Solve it!



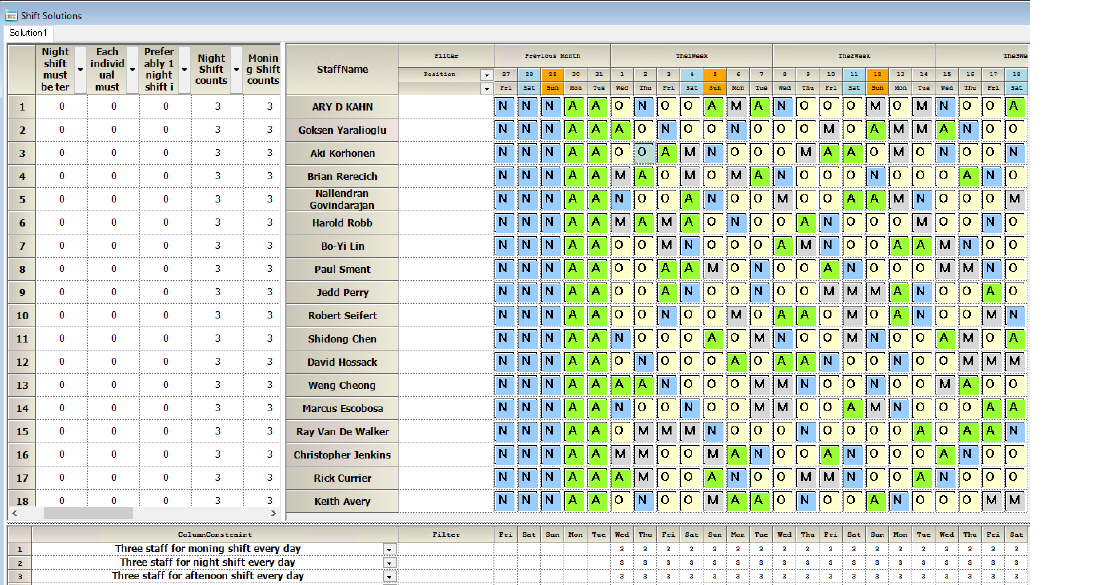
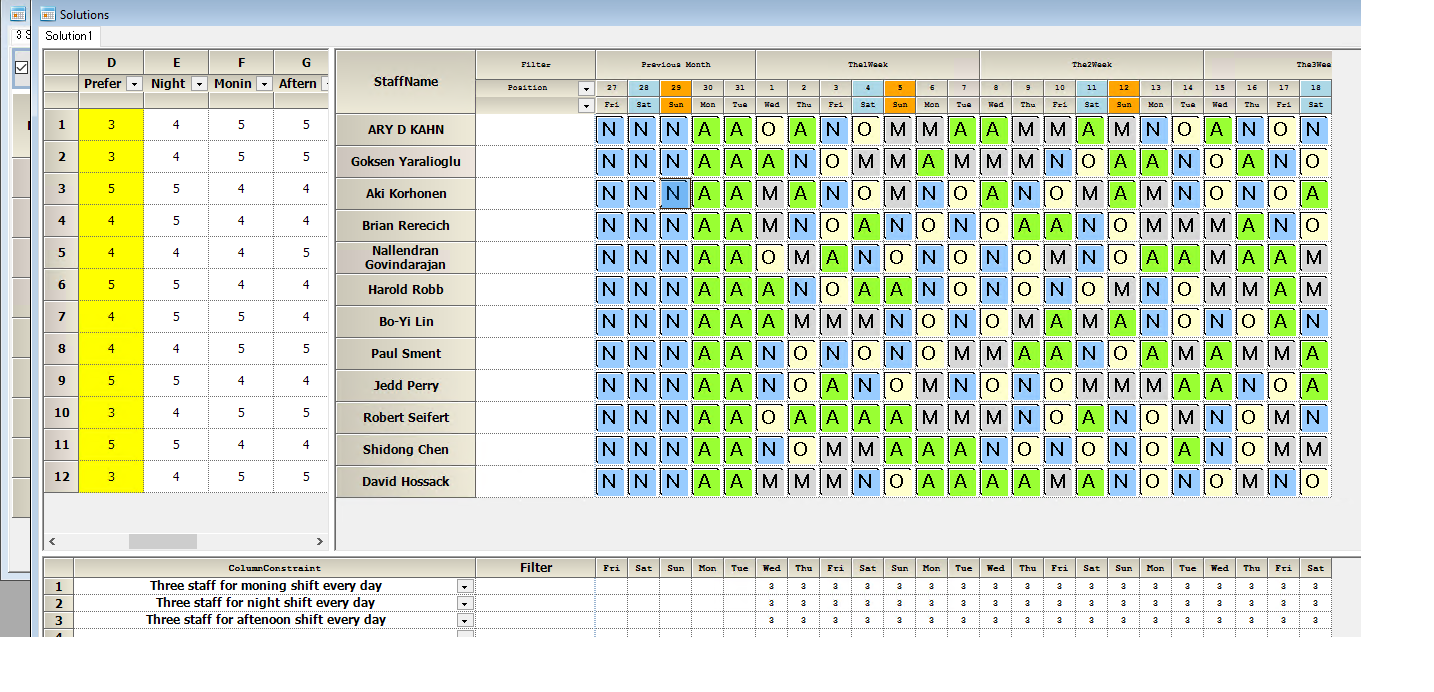
Solution staff 12

We see no two days rest due to shortage of staff resources.



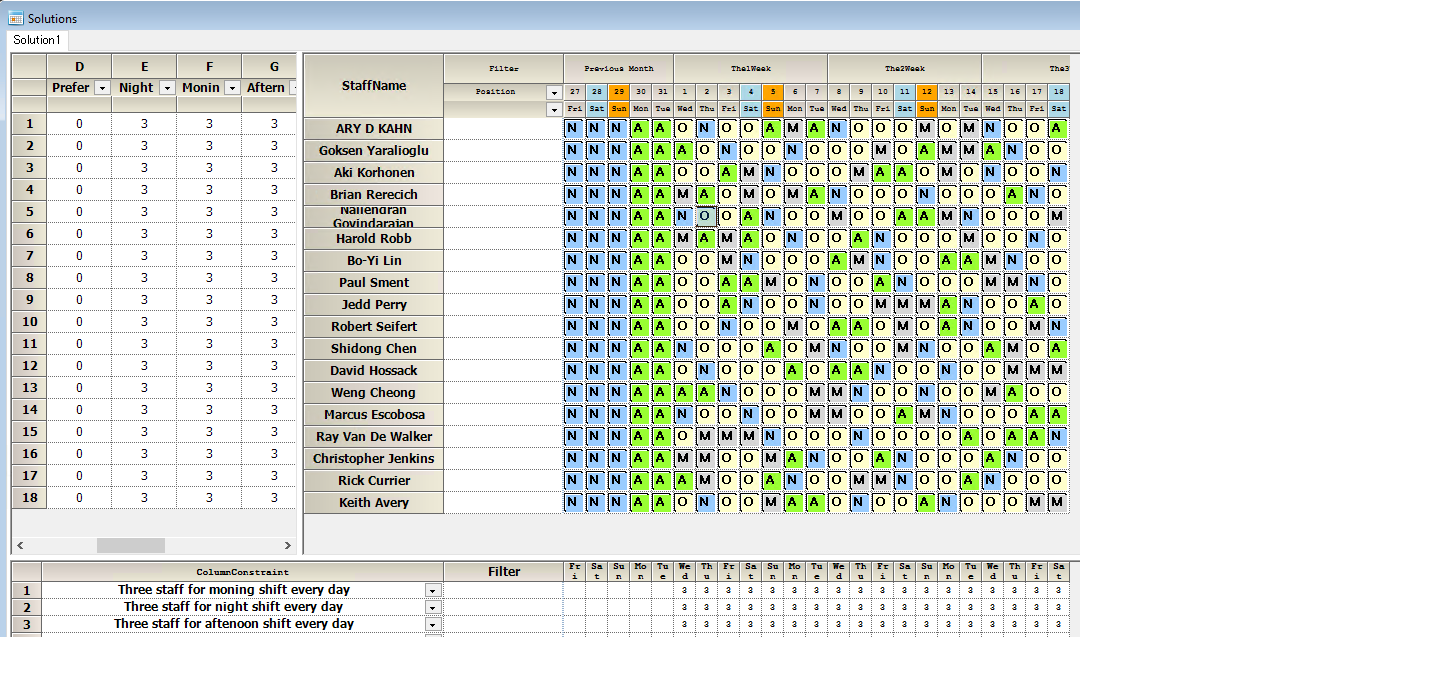
Solution staff 18

We see every staff can get more fabulous than or equal to two days rest.
The objective function value becomes zero, as shown the fig. above.



Load the Project File

File → Open Project File from GitHub